Camera Intrinsic Parameter
The
idiom calibrating intrinsic camera parameters means finding the transformation
from camera 3D coordinate system to image 2D coordinate system (using projection
matrix). Where:
§ Camera
Frame: is the coordinate system which takes camera center as its origin and the
optic axis as (Z), and is in mm.
§ Image
Frame: is the coordinate system which measures the pixel location in the image
plane (only x and y) and its origin is the above left corner of the chip.
o Camera
intrinsic Parameters characterize the optical, geometry and digital characteristics
of a camera.
o The
degree of freedom of Intrinsic parameter in the real situation (not ideal
situation) is 5:
§ Sx,
Sy (sometimes called:
) are the pixel scale factors (pixel à mm) in x and y direction (can be expressed by focal length and aspect
ratio) Aspect ratio: is the ratio of pixel size difference between x and y
(width and length) in ideal situation is 1.
§ V0
and U0: are the deviation of sensor position with reference to
retinal plane.
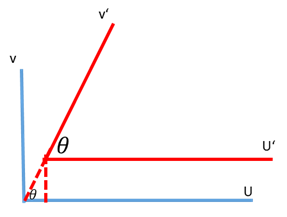
§
: is the skew factor: which is how much u and v vectors are perpendicular
to each other’s. Is 90 degree in the ideal situation, so and from the small
triangle we can say:
§ Based
on these factors and taking these factors into consideration and using the
following diagram, we can write the intrinsic calibration matrix (projection
matrix) in the real situation (NOT in ideal situation):
Based on that we can write the intrinsic parameter matrix (to get u and
v, we divide the result by z).
o Now,
assuming we have square pixels (aspect ratio=1) and there is no skew (both u
and v are perpendicular s=0) and optical center of the chip is in the middle of
retinal plane (cx and cy=0), we get to ideal situation matrix (Pro_4) which has
only ONE degree of freedom which is focal length f.
o Another
way to express the above theory is: The transform between camera Frame (in mm)
and Image Frame (in Pixel) is calculated by:
§ X,Y:
are the point coordinates in camera frame in mm.
§ Xim,
Yim or (u,v): are pixel values of the point in image frame in pixels:
expressed as u and v
§ Ox,
Oy: are the principle point position (Hauptpunkt) in image frame in
pixels (which is usually the half of image length and width)
§ Sx,Sy:
effective size of pixel in mm in both horizontal (x) and vertical directions
(y).
The above equation, is the
equation which is used to calculate the transformation from 2D (Image Frame) to
3D Camera World Frame the Z can be obtained from Stereo concept
From the above illustration we see that:
o M
is a point in a 3D space, where its coordinates are known (x,y,z). the x,y of
the point are exactly the x,y on the image which are calculated from the
equations (Pro_1 and 2)
o π is the retinal plane (a plane where the lens
reflects the points), (u,v) are the coordinates system of the retinal plane in
pixel
o Then
the two coordinates systems are connected via this equation
§ Remember:
u,v are in pixel, x,y: are in mm
§ Remember:
we write –f because x and u are on the same direction, v and y are also on the
same direction BUT Z is going out while f is to the inside the camera so we
have –f:
o The
(Pro_3) is written linearly in homogenous coordinates system (This is the Intrinsic
Calibration Matrix “Projection Matrix”):
Let us apply this in a small example using Python:
# -*- coding: utf-8 -*-
"""
@Author: Mohanad Sawas
@Project: Projecting a 3D point in mm to a 2D point in pixel using
projection matrix
"""
#importing numpy in order to manipulate matrices
import numpy as np
# define a function which will return the point in 2D and takes a 3D
point and focal length as input
def project_point(p,f):
#first we write projection
Matrix which is a 4*3 matrix
M=np.array([[f, 0, 0, 0],[0, f,
0, 0],[0, 0, 1, 0]])
#now we convert the p point to
homogenious form by adding 1 and transpose it to get it as a vector
p_homo=np.append(p,1)
p_homo=np.transpose(p_homo)
#the projected point is a
result of projection matrix multiplication with 3D point
P_projected=np.dot(M,p_homo)
#finally the result is the
point in homogenious form, and it should be returned back to the
non-homogenious form by dividing on Z:
point2D=[P_projected[0]/P_projected[2], P_projected[1]/P_projected[2]]
return point2D
# Testing the function
p=[100,200,50]
f=50
print("The Projected point is:
",project_point(p,f))










Comments
Post a Comment